After I spend 2-3 days teaching integer addition (click here to read my post on adding integers) and am confident my students are comfortable with it, I move onto subtraction.

I start by giving students two color counters again and put an easy question on the board for them to solve independently:

-5 – (-2)

Since students are familiar with subtraction meaning “take away”, they are able to solve this problem without any assistance.  They start with 5 red 2-color counters and take 2 away, so they are left with 3 red counters (or -3).

I always hear “this is easy!” at this point, but that sentiment goes away quickly when I give them the next problem:

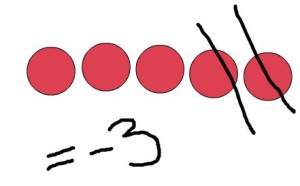
-5 – 3

This one is not so easy for them.  They start with 5 red counters again but this time they need to take away 3 yellow ones, which is obviously impossible since they don’t have any yellow ones to begin with.  When I ask the class how I am going to take away 3 yellow if I don’t have any yellow to begin with I usually hear the following two responses:

1. “Just flip 3 of the counters over to the yellow side and then take them away”.  I ask the class why I can’t just flip 3 of the counters over and someone is always able to tell me that if I flip 3 of them over, I have now changed the -5 to a +1, so it’s a completely different problem now.  (Sometimes I have to actually demonstrate this for them to see it).
2. “Just add 3 yellow ones to the -5 and then take them away”. Again I ask the class if this makes sense and someone is able to tell me that  I have now changed the -5 to a -2 if I add 3 yellows to it, so once again it is a completely different problem.

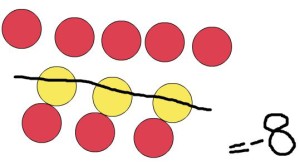
After seeing those two suggestions fail one of my students is able to figure out what to do…instead of just adding 3 yellow ones to it, I should add 3 yellow and 3 red to it because that is essentially just adding zero to the -5 three times, which isn’t changing it at all.  (This is why it is really important to drive home the concept of zero pairs when teaching integer addition!)   Once I add those counters to the -5, I am able to take away 3 yellow ones to finish solving the problem, and am left with 8 red counters (or -8).

I usually do one more problem with the class to make sure they get the concept of adding zero pairs so that they can take away what they need to take away.  Then I have them practice several problems on their own:

-8 – (-6)

-4 – 2

3 – (-7)

10 – 12

-5 – 4

-9 – (-7)

1 – 5

2 – (-3)

Once they are done using the counters to solve the problems, we check the answers as a class, and I ask the class to come up with a rule that they can use to solve the problems without 2-color counters.  It sometimes takes a little guidance from me, but eventually we come up with the rule that subtracting integers is really the same as adding the opposite.  I have them write our “official” rule in their notebooks along with some examples.

We shorten the rule to “keep, change, change”, since they are keeping the first integer the same, changing the subtraction to addition, and changing the second integer to its opposite.  The students love this rule because after they do “keep, change, change” they are just solving an integer addition problem, which they already know how to do!

I assign subtraction problems for homework that use small numbers so that they can use counters if they want.

The next class period, I have the students practice integer subtraction with partner worksheets and/or self-checking worksheets and I assign problems with large numbers for homework the second night so that they are forced to use the “rule” instead of 2-color counters.

The following day I have the students practice both integer addition and subtraction.  I never used to take an extra day to review both operations but I found that some students are good when they are just adding or just subtracting, but get mixed up when they have a combination of the two operations.

To review both operations, I break the class up into 3 groups and do centers.  I have one group working with me on mini whiteboards solving integer addition and subtraction problems.  I have another group working on integer addition & subtraction self-checking task cards.  (I love, love, love self-checking activities because they allow the students to see for themselves if they know what they are doing!)  I have the third group playing a Bingo game on adding & subtracting integers.  I have found this stations day to be very valuable in giving students the practice they need with adding and subtracting integers and the kids always enjoy it!

I move onto integer multiplication & division the next day (which I will write about in my next post).

If you are interested in checking out the self-checking task cards or bingo game I use on adding & subtracting integers, click the images below.

Thanks for reading,

Christina