I wrote a blog post 2 years ago about using the cake method to find the GCF & LCM of 2 numbers. (I absolutely LOVE this method and my students have had alot of success with it!) I have been meaning to follow up on that post by sharing how to use this method for more than 2 numbers, and since I just got a question about this last week, I figured now is the time to write that post. 🙂
For this example, I will find the greatest common factor & least common multiple of 12, 15, & 18.
Start by writing the 3 numbers next to each other and drawing a “layer of cake” around them. Take out any number that you can divide all three numbers by (in this case 3). Then divide the numbers by 3 and write the quotients under the original numbers, drawing another layer of cake around them. If there is something else you can divide all 3 numbers by, repeat this process. In this case, though, there is nothing (besides 1) that I can divide 4, 5, & 6 by so at this point I like to CHANGE COLORS. Now you need to find if there is any number you can divide some of the numbers by. In this case, I can divide 4 and 6 by 2, so I write a 2 on the side (in a different color) and then divide the 4 and 6 by 2. Since I am not dividing the 5 by anything, I just bring it down. Repeat if you can divide some of the numbers by another factor. In this case, I can’t, so I am done.
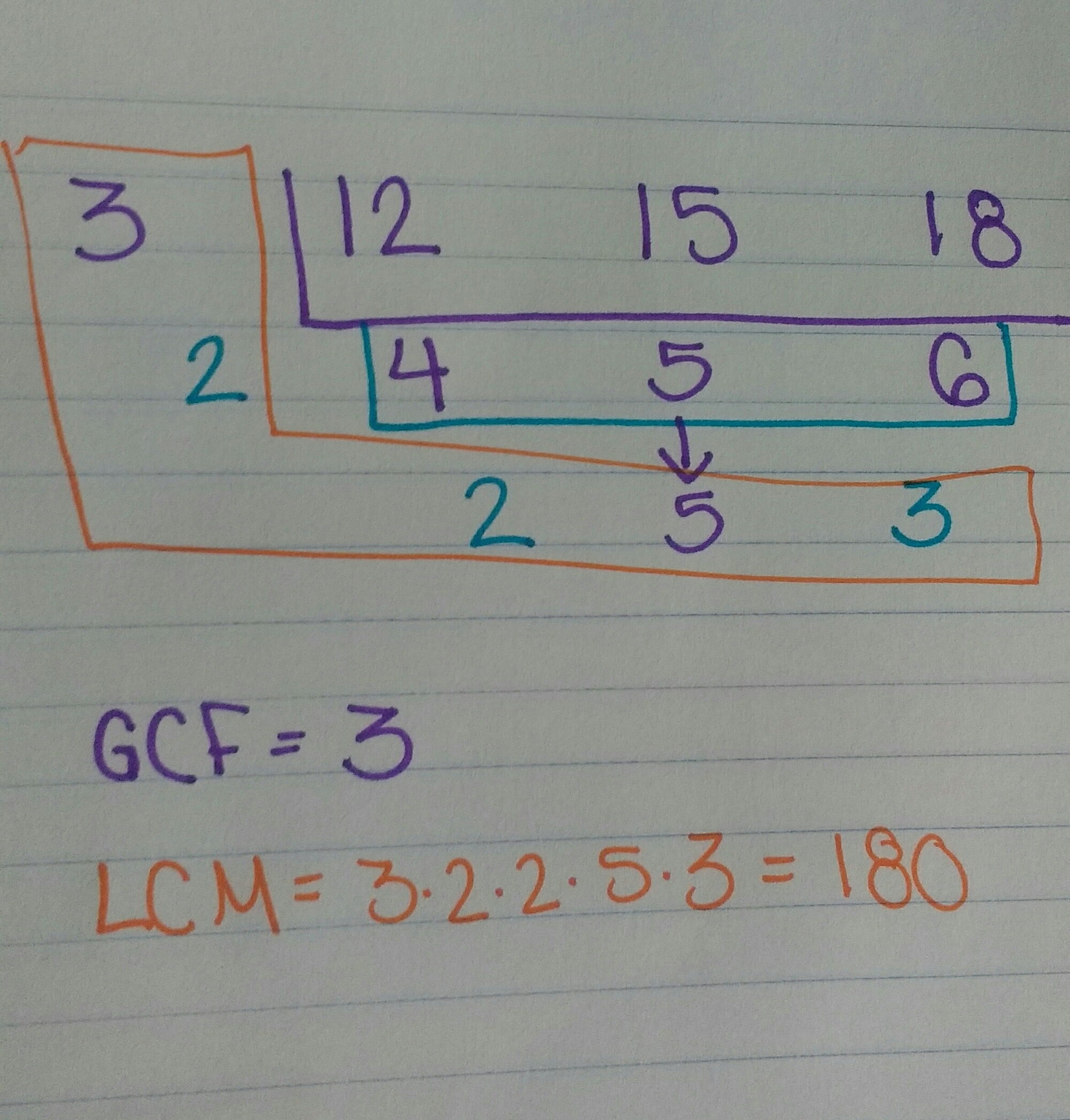
Find the GCF by multiplying all the numbers on the left that were in the ORIGINAL color ONLY! (In this case, it is only “3”, so my GCF = 3). Find the LCM by multiplying all of the numbers in the “big L” around the cake. (That includes the numbers in both colors). (For this example the LCM = 3 x 2 x 2 x 5 x 3 = 180).
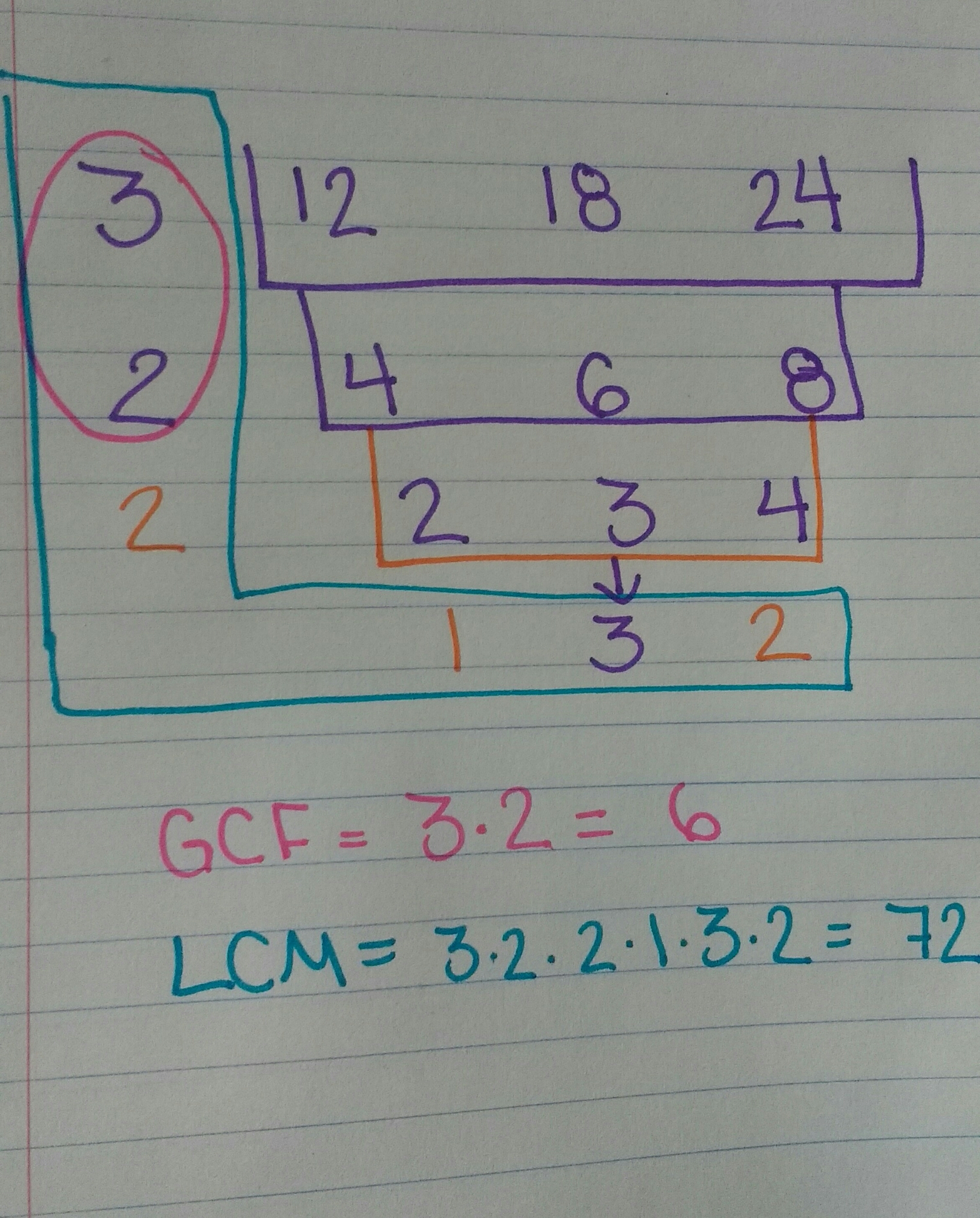
In case my explanation makes no sense, I have included a second example showing this process.
As I said, I absolutely LOVE the cake method and have found that the students love it too and find it MUCH easier than other methods for finding the GCF & LCM. I hope this post helped explain how to use it for more than 2 numbers!
Thanks for reading,
Christina
You also may be interested in my GCF & LCM Halloween Riddle Sheet – available in my TpT store for $1.


thanks for clarifying to “Switch Colors” and only including those in original as GCF!!!
I’m glad it helped!
Pingback:But really, what goes on in your classroom? – Mrs. Karner's Class Blog
Thank you. You are really clever and creative. And the explanation is crystal clear.
This really helped! Thanks for the tip about the GCF only multiplying the original colors.
This method is really cool! I have never seen this method before. Did you come up with this method yourself? Very clever!
I agree that it’s very cool! I did not come up with the cake method myself. The first time I saw the cake method was when I read Danika McKellar’s book “Math Doesn’t Suck” about 10 years ago. (I had not seen anything about using it for the gcf & lcm of 3 or more numbers anywhere so I just thought about how to adapt it and came up with this.)
Hi, I use this method a lot but I have found a anomaly that I can’t explain. (I know these are low numbers but they are just an example)., if I want to know the LCM of 3, 6, & 4 I can use the prime factor of 2 and bring the 3 down to the next level making2* 3, 3, 2 that now gives a LCM of 36, but 12 is in fact the LCM. What is going wrong?
Hi Stephen,
Thanks for the question! The issue you are running into here is that you haven’t completed your “cake” since after that first step you still have a gcf for two of the remaining numbers since you now have two 3’s along the bottom. Therefore, you should make another layer, pulling a 3 to the left, giving you 1, 1, 2 along the bottom. So, your LCM would be (2*3)*(1*1*2) = 12.
I hope that helps!
Thanks,
Christina