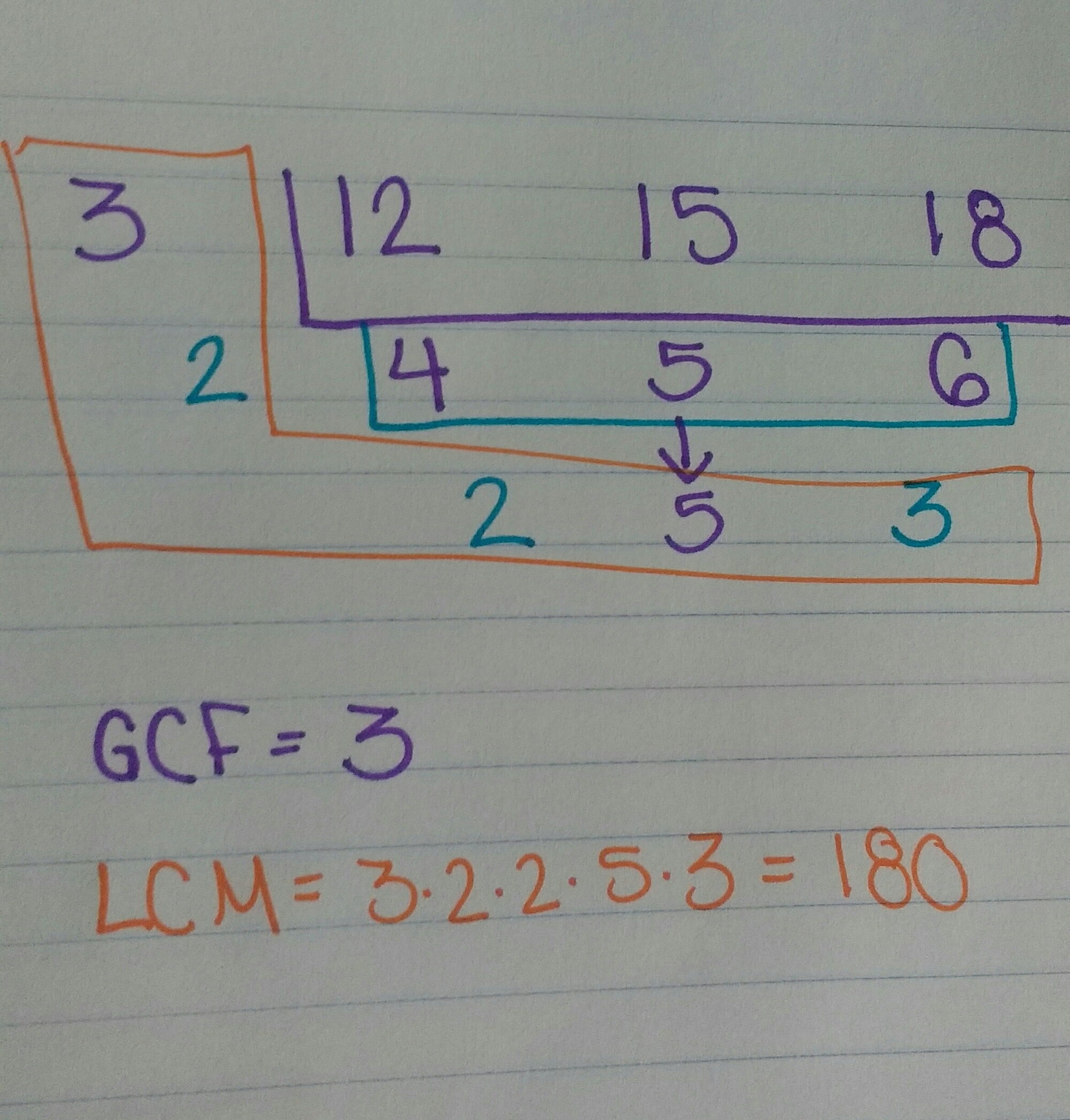
Finding the GCF & LCM of 3 or More Numbers using the Cake Method
I wrote a blog post 2 years ago about using the cake method to find the GCF & LCM of 2 numbers. (I absolutely LOVE this method and my students have had alot of success with it!) I have been meaning to follow up on that post by sharing how to use this method for moreRead more about Finding the GCF & LCM of 3 or More Numbers using the Cake Method[…]