Finding the GCF and LCM using the Cake Method

/ / 18 comments

Today’s lesson in my 7th grade math class was on finding the greatest common factor and least common multiple of a pair of numbers.

I started by gathering background information about what the students already knew about the GCF and LCM.  With a little bit of help the students were able to come up with definitions for each of them and described the method they had used in the past to find the greatest common factor and least common multiple of two numbers.

Previously the students had learned to list all the factors of 2 numbers and find the largest one they had in common.  Similarly, to find the least common multiple, the class had learned to list multiples of the numbers until they found one in common.

We went through examples of finding the GCF and LCM the “old school” way by listing factors and multiples of numbers and finding the ones they have in common.

Then we discussed the limitations of this method for finding the GCF and LCM, mainly the fact that if I gave them much larger numbers it would be very time-consuming to list all the factors or list multiples until they found one in common.  So…I then introduced the class to the “Cake Method”.  (Alot of people refer to it as the ladder method or division ladder, but I first saw it called the cake method in the book Math Doesn’t Suck by Danika McKellar, and I thought it was cute, so that is what I go by, since it resembles an upside-down cake).

The cake method is great for a couple of different reasons…you can make one “cake” and use it to find both the GCF and the LCM and it saves you alot of time over the more traditional method.

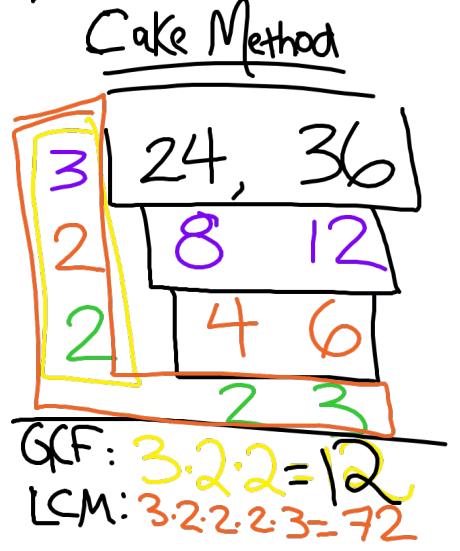
For anyone who hasn’t seen this method before, you start by writing the numbers for which you are trying to find the GCF and LCM next to each other and draw a “layer of cake” around them.  You then find ANY common factor of the two numbers and write that factor to the left of them.  You then divide the numbers by their common factor and write the quotients underneath the numbers.  This process repeats then with the new 2 numbers you have inside the cake.  You do this as many times as necessary until the 2 numbers at the bottom are relatively prime.  To find the greatest common factor, you multiply all the numbers to the left of the cake.  To find the LCM, I tell the students to draw a big “L” around the cake, and multiply all the numbers in the “L” together.

Here is the example we did in class to find the GCF and LCM of 24 and 36.

cake method

 

We had a discussion about how different people could make different “cakes” by choosing different factors, but that the final answer would be the same.  We also discussed how the bigger the factor, the less layers of cake there would be.

Overall, the lesson went great!  The students loved this “new” method of finding the GCF and LCM!

I am looking forward to showing them how the cake method can be used to simplify fractions, too.  (Make a cake for the numerator and denominator and the 2 relatively prime numbers at the bottom will be the simplified fraction.  For example, the cake example above could have been used to simplify the fraction 24/36 to 2/3.)

 

18 thoughts on “Finding the GCF and LCM using the Cake Method”

  1. We call this the “ladder method” in my school, but I love it. I think it is SO easy for myself and the kids. It’s one of those “Why didn’t my math teacher show me this!?” things.

    Reply

  2. I agree! The only method I learned in school was the list method…this is so much easier and faster! Don’t know why my teachers never taught it to us…

    Reply

  3. Thank you so much for the clear explanation. My kid has been in tears struggling with LCM cos her mind just freezes upon large numbers and I was clueless about how to help her. Your method is much more manageable and the cake image will lift her spirit.

    Reply

    1. I’m so glad that you can use this to help your daughter with the LCM! I appreciate you taking the time to leave me a comment! 🙂

      Reply

  5. Why on earth don’t they teach it this way in school??? I’m a homeschool mom now and this is how I will be teaching my own kids. So much simpler!

    Reply

  6. Pingback:5 Ways to Use Factor Trees in Middle School Math | Math in the Middle

    1. Hi Gabby,

      I teach my students what it means for two numbers to be relatively prime and we discuss how/why the LCM of relatively prime numbers is their product.

      However, if you want to use the cake method for two relatively prime numbers, it will still work. Just pull out a 1 on the side and divide each of the numbers by 1 (so they won’t change). The gcf will be 1 and the LCM will be 1 * the two numbers.

      Hope that helps!

      Thanks,
      Christina

      Reply

  8. Anyone have difficuluties using this method to find LCM of 3 or more numbers? My students and I discovered it only seems to work for finding the LCM of 2 numbers

    Reply

    1. Hi Rita,

      For 3 or more numbers you can find the LCM of two and then find the LCM of that answer and the 3rd number.

      There is a way to do 3 numbers at once with the cake method, as well, but I don’t think it would make sense if I tried to explain it in words…

      I had planned to write a blog post on it at some point and never got around to it. I will try to write one this week on using this method for more than 2 numbers.

      Thanks,
      Christina

      Reply

  10. I don’t see how this method would work if you were trying to find the GCF and LCM of three numbers, like 6, 8, and 12.

    GCF = 2
    LCM = 24

    Reply

    1. To find the prime factorization of a number, make a “cake” with the number on the inside. Pull out a prime factor of the number on the left and then divide by that number to make the next layer. Repeat with more layers until you get down to 1 in your last layer. The prime factorization is the product of all of the numbers to the left of the cake.

      Hope that helps!

      Thanks,
      Christina

      Reply

Leave a Reply