I am a HUGE fan of group work! I love having students work together in my math classes for practice work, problem solving, review games, etc. Occasionally I allow my students to pick their own groups, but more often than not I assign them because:
- No students are ever left out or the last one picked when I assign them
- I can make sure the groups are either mixed ability levels or homogenous (whatever I need for a particular class period)
I pick new groups every time we do group work because I think it’s important for the students to be able to work successfully with different people and I don’t want students “stuck” with the same people every time. I have done different things in the past to pick random groups such as having the students count off or handing them playing cards as they walk in the room. I also have deliberately placed students in groups. But I was looking for a way to mix things up…
…so I have come up with the following solution: As the students come into the classroom I will hand them a card with a math problem they need to solve (relating to what they are learning). This problem will be in place of the typical do now problems I give them on Socrative. Once they solve the problem, they will need to find the table labeled with the answer to their card, and sit there. (3 other students’ cards will have that same answer), so those 4 students will be a group for the day. (I will be walking around to assist any students who struggle with their problem).
I am pretty excited to try this and can think of a bunch of different ways to change this up. I could have the groups be completely random by just giving each student a random card, or I can make the “random” groups fit my needs based on ability level (without the students even realizing it) by grouping the cards based on difficulty level and giving each student a card from the group that is appropriate for them. [If I want mixed ability level groups, the 4 cards with matching answers will be 4 different difficulty levels; If I want homogenous groups, the 4 cards with matching answers will be the same difficulty level.]
Obviously this will require a bit of prep time in advance (since I have to come up with the questions), but I plan to laminate the cards and use them every year. I can also re-use them as a card-sorting center activity, as task cards, game cards, etc., so I think that it is worth the initial time investment. (There are soo many different ways that I can use and re-use the cards!!)
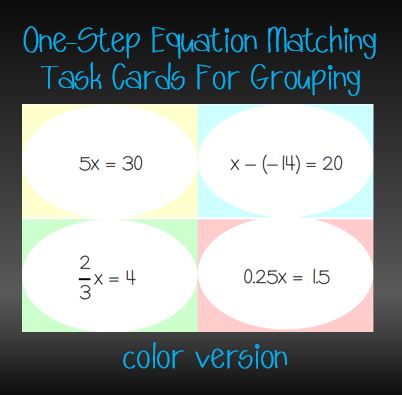
I made my first set of these cards on one-step equations and have them set up to create mixed-ability level groups. I color coded the cards by difficulty level – yellow include only whole numbers, blue include integers, green include fractions, and red include decimals. As the students walk in the class, I will give the students who struggle with one-step equations yellow cards, and the students who need more of a challenge green or red. The groups will end up with one of each color card, giving me random, but “equal” mixed-ability level groups.
You can grab this set of 32 matching task cards (to form up to 8 groups of 4) on one-step equations FREE by clicking the download links below. (I included the color-coded cards and the same cards in black and white…feel free to download and use whichever version you prefer).

Do you have any other ideas of how to use these matching cards? Please leave me a comment with your thoughts!!
Thanks for reading,
Christina


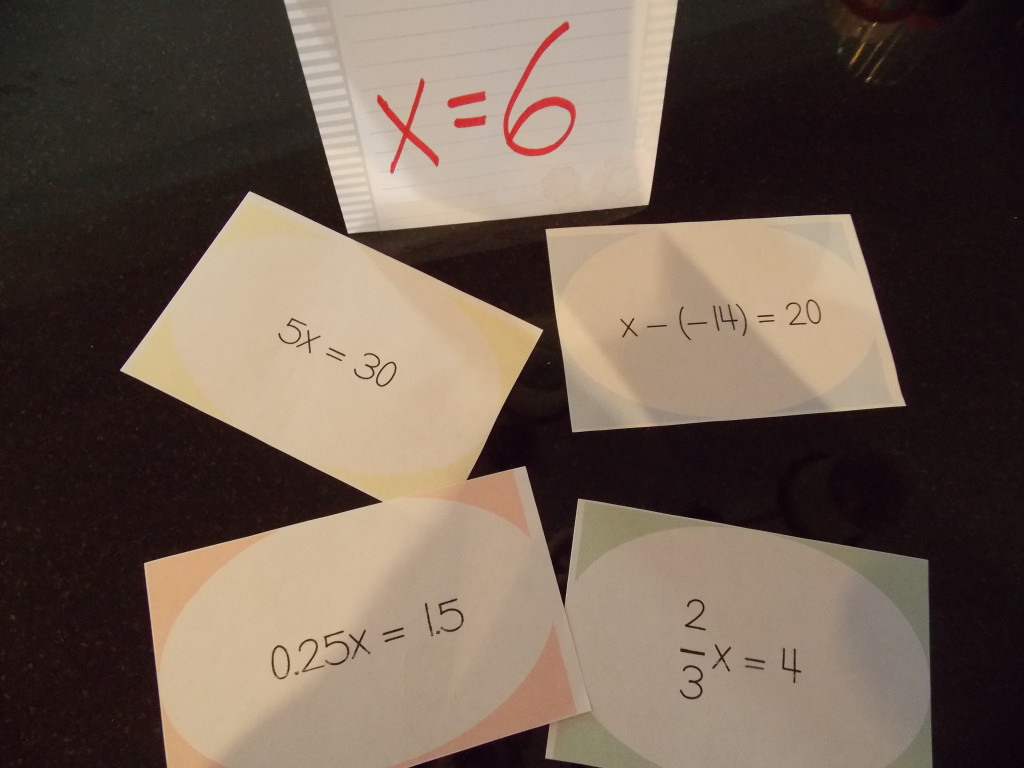
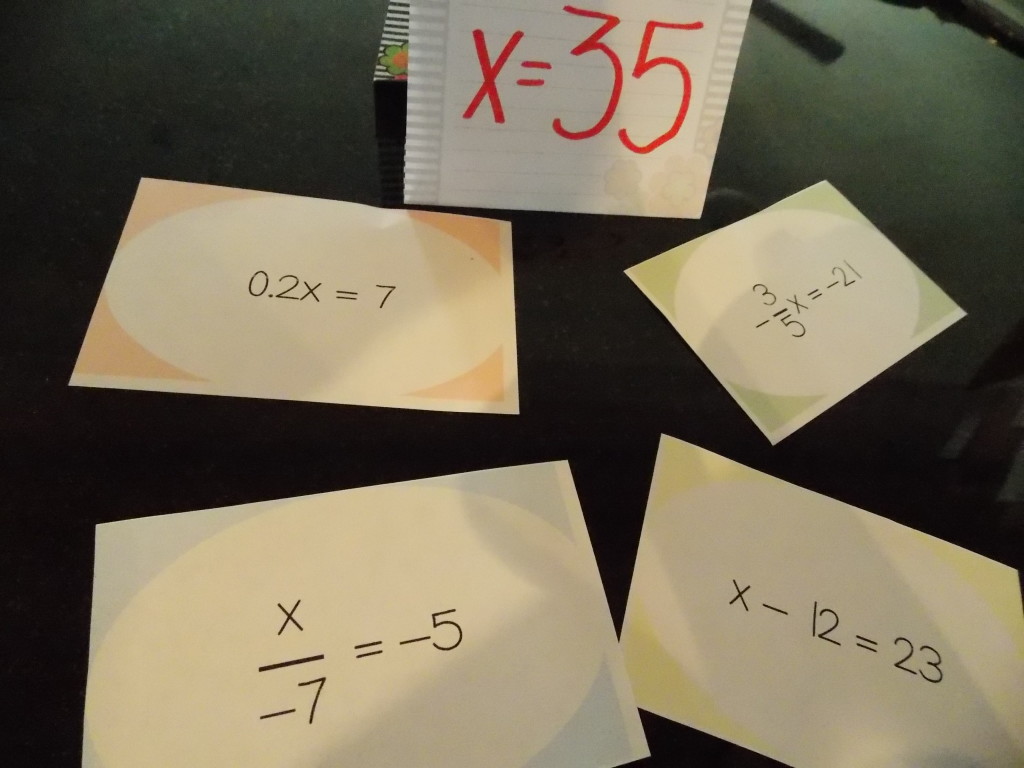

I will sometimes let students choose a card from a deck of pre-selected cards. Then students may be based on the chosen suit, or card value. For example, if I want 4 groups, then students will be grouped based on their suit. If I want more than 4 groups, I will have all of the “2’s or J’s” in a group. With either approach, I’ve already decided how many groups I want and I’ve pre-determined which cards will be available for the students to choose from.
I agree that using a deck of cards is a great, quick way to break the class into random groups when you are not specifically looking for mixed ability levels or homogenous groups. Thanks for sharing!
Pingback:12 One Step Equation Activities That Are Out of this World - Idea Galaxy
How do you pass out the cards to a class of 30 as they enter and keep track of which students you want in each group? This seems like a great way to randomly assign groups but I don’t see how to use it for intentional groupings.
Hi Alicia,
I wouldn’t pre-select which specific kids I want in the same group using this method. However, it is easy enough to give certain kids yellow cards and other kids red cards, for example, as they walk in. I won’t know which group they will end up in but if I give all my struggling students yellow and all of my top kids red cards, etc. that will ensure that each group ends up with one of my top students and one of my struggling students since I know each group is made up of 4 different color cards. Not sure if I explained it well…Does that make sense?
Thanks!
Christina