Today I’m writing about a simple idea that makes 2-step equations easy for kids – a box “trick”.

Students obviously have already learned how to solve one-step equations before being introduced to two-step equations, so I introduce 2-step equations by giving students a simple one-step equation.  The only difference is that I use an index card instead of a variable in my equation.

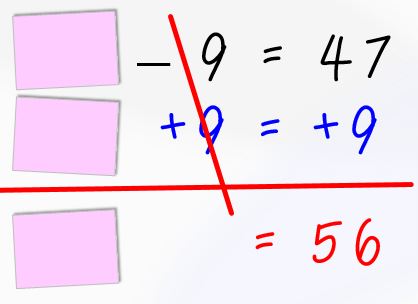
Put an equation like the one pictured above on the board and tell students to solve it for the index card, which they should be able to do easily since it is a simple one-step subtraction equation.

Once they solve the equation for the index card, lift up the original card to reveal what is underneath it (in this case 8x).  It also works if you write 8x on the backs of the index cards and just flip them over.

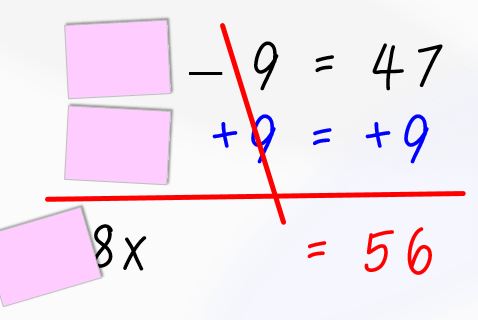
So, since the index card = 8x they now need to solve the equation 8x = 56, which is another simple one-step equation that they should already know how to solve.

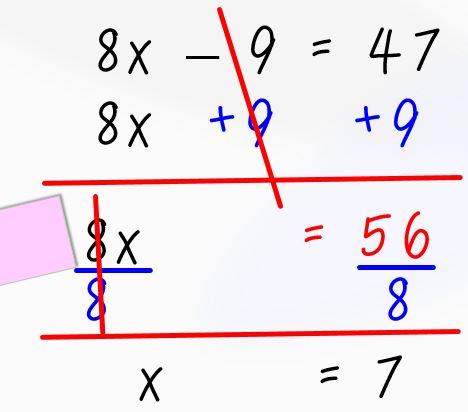
Do another example or two with the class and then discuss how to decide which part of the equation goes under the index card (whichever part comes first using the order of operations).  Have students replicate the process in their notebooks by giving them a 2-step equation.  They need to draw a box around the part that would be under the index card.  First solve the equation for the box and then solve the new equation for the variable.

I have found that this method really helps students make sense of solving 2-step equations by turning them into two 1-step equations.  How do you introduce 2-step equations in your class?  Do you do something similar?  Please share in the comments!

If you are in need of resources to supplement your lessons on one and two step equations you may be interested in the following activities in my TpT strore:

Thanks for reading,

Christina